Удиви меня

Log x 2 8x 7

Log^2 2 3+log2 12:log12 2-log2 144: log3 2. Log 2 4+ х log 2 -x +2. Log x 2 8x 7. Лог 3 5 лог 3 7 лог 7 0. Log3 x 1 меньше или равно 2.
Log^2 2 3+log2 12:log12 2-log2 144: log3 2. Log 2 4+ х log 2 -x +2. Log x 2 8x 7. Лог 3 5 лог 3 7 лог 7 0. Log3 x 1 меньше или равно 2.
Log2(7-х)=2log8 3. Log7x=2. Решить уравнение log. Log4 2 x 1 x-1 1. 02 лог 8 (2x) +log8(x2+1-2x) =4/3.
Log2(7-х)=2log8 3. Log7x=2. Решить уравнение log. Log4 2 x 1 x-1 1. 02 лог 8 (2x) +log8(x2+1-2x) =4/3.
Введение новой переменной логарифмических уравнений. Лог 2 x> 1. Лог 2 4. Log x 2 8x 7. Log 1/7 7-x -2.
Введение новой переменной логарифмических уравнений. Лог 2 x> 1. Лог 2 4. Log x 2 8x 7. Log 1/7 7-x -2.
Log2(x-2)+log2(x-3)=1. Log 1/2 x. X меньше 2. Log7 x 1 log7 x log7 x. Лог 0.
Log2(x-2)+log2(x-3)=1. Log 1/2 x. X меньше 2. Log7 x 1 log7 x log7 x. Лог 0.
Log x 2 8x 7. Log x 2 x-1 2 меньше или равно 1. Log3(1-2x)=1. Log3 (6 5x)- log3 4 5x 2 вариант. Log x 2 8x 7.
Log x 2 8x 7. Log x 2 x-1 2 меньше или равно 1. Log3(1-2x)=1. Log3 (6 5x)- log3 4 5x 2 вариант. Log x 2 8x 7.
Log7x > 1. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x. Log2(2x-1)=3 решение. Log x 2 8x 7. Log 2 (x 2 -2) - log 2 x <= log 2 (x-2 /x 2).
Log7x > 1. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x. Log2(2x-1)=3 решение. Log x 2 8x 7. Log 2 (x 2 -2) - log 2 x <= log 2 (x-2 /x 2).
Лог 3 5 лог 3 7 лог 7 0. Log_3⁡〖1/х〗 +log_3⁡〖(х^2 〗+3х-9)≤log_3⁡〖(х^2 〗+3х +1/х – 9). Log5 7 x log5 3 x +1 одз. Log2(log2x)=1. Log x 2 8x 7.
Лог 3 5 лог 3 7 лог 7 0. Log_3⁡〖1/х〗 +log_3⁡〖(х^2 〗+3х-9)≤log_3⁡〖(х^2 〗+3х +1/х – 9). Log5 7 x log5 3 x +1 одз. Log2(log2x)=1. Log x 2 8x 7.
2лог2(х) 3лог3х. Log x 2 8x 7. Log x 2 8x 7. Log x 2 8x 7. 7 log x 2-2x-8 8+log12.
2лог2(х) 3лог3х. Log x 2 8x 7. Log x 2 8x 7. Log x 2 8x 7. 7 log x 2-2x-8 8+log12.
Log x 2 8x 7. Log0,5(x2-3x)=-2. Лог 3(х-7)=лог 2(2х+1). Log2. Log x 2 8x 7.
Log x 2 8x 7. Log0,5(x2-3x)=-2. Лог 3(х-7)=лог 2(2х+1). Log2. Log x 2 8x 7.
Log2 2. Log2(x-5) меньше 2. 7log12 x 2-2x-8 8+log12 x+2. 2. Log2x.
Log2 2. Log2(x-5) меньше 2. 7log12 x 2-2x-8 8+log12 x+2. 2. Log2x.
10 log10 2. Log0,1(6 − 6x) ≤ log0,1 (x 2 − 4x + 3) + log0,1(x + 4). Log x 2 8x 7. Log x 2 8x 7. Лог 3 х2-х-3 лог 3 2х2+х-3.
10 log10 2. Log0,1(6 − 6x) ≤ log0,1 (x 2 − 4x + 3) + log0,1(x + 4). Log x 2 8x 7. Log x 2 8x 7. Лог 3 х2-х-3 лог 3 2х2+х-3.
Log 1/2 x. Log2x=3. Log7 x2 12x 4 log7 8 x. Log x 2 8x 7. Метод введения новой переменной логарифмические уравнения.
Log 1/2 x. Log2x=3. Log7 x2 12x 4 log7 8 x. Log x 2 8x 7. Метод введения новой переменной логарифмические уравнения.
Log 1,6 log 0,5 x2-x-6. Лог 7 х > 1 лог 7 х > -1. 2log2 (2x-2) <= x. Решение log*log. Log2x.
Log 1,6 log 0,5 x2-x-6. Лог 7 х > 1 лог 7 х > -1. 2log2 (2x-2) <= x. Решение log*log. Log2x.
Log x 2 8x 7. Log2(х2 + х) = 1. Log2. Лог1/3 х>4. 〖1+log〗_2 (х-1)=log_((х-1))⁡4.
Log x 2 8x 7. Log2(х2 + х) = 1. Log2. Лог1/3 х>4. 〖1+log〗_2 (х-1)=log_((х-1))⁡4.
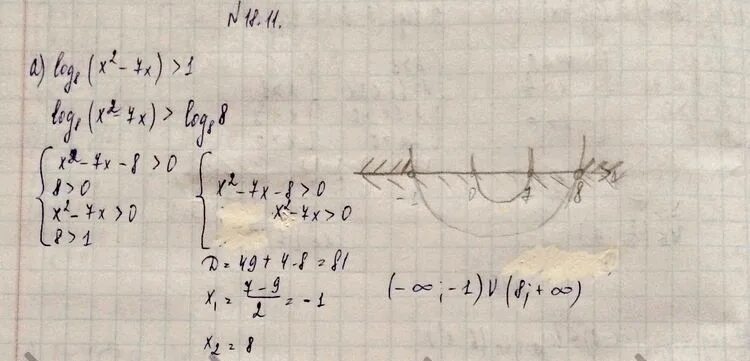Сравнить log1/2 1/3 и log1/3 1/2. Лог1/7 7-х -2. Log x 2 8x 7. Log2 2. Log 2 2 x - log 2 x-2.
Сравнить log1/2 1/3 и log1/3 1/2. Лог1/7 7-х -2. Log x 2 8x 7. Log2 2. Log 2 2 x - log 2 x-2.
Log x 2 8x 7. Логарифмические уравнения log12 (x^2-x)=1. Log12(x^2-x)<1 решение. 4^{2\log_2 3-1}4 2log 2 3−1. Пример уравнения логарифм в степени логарифма.
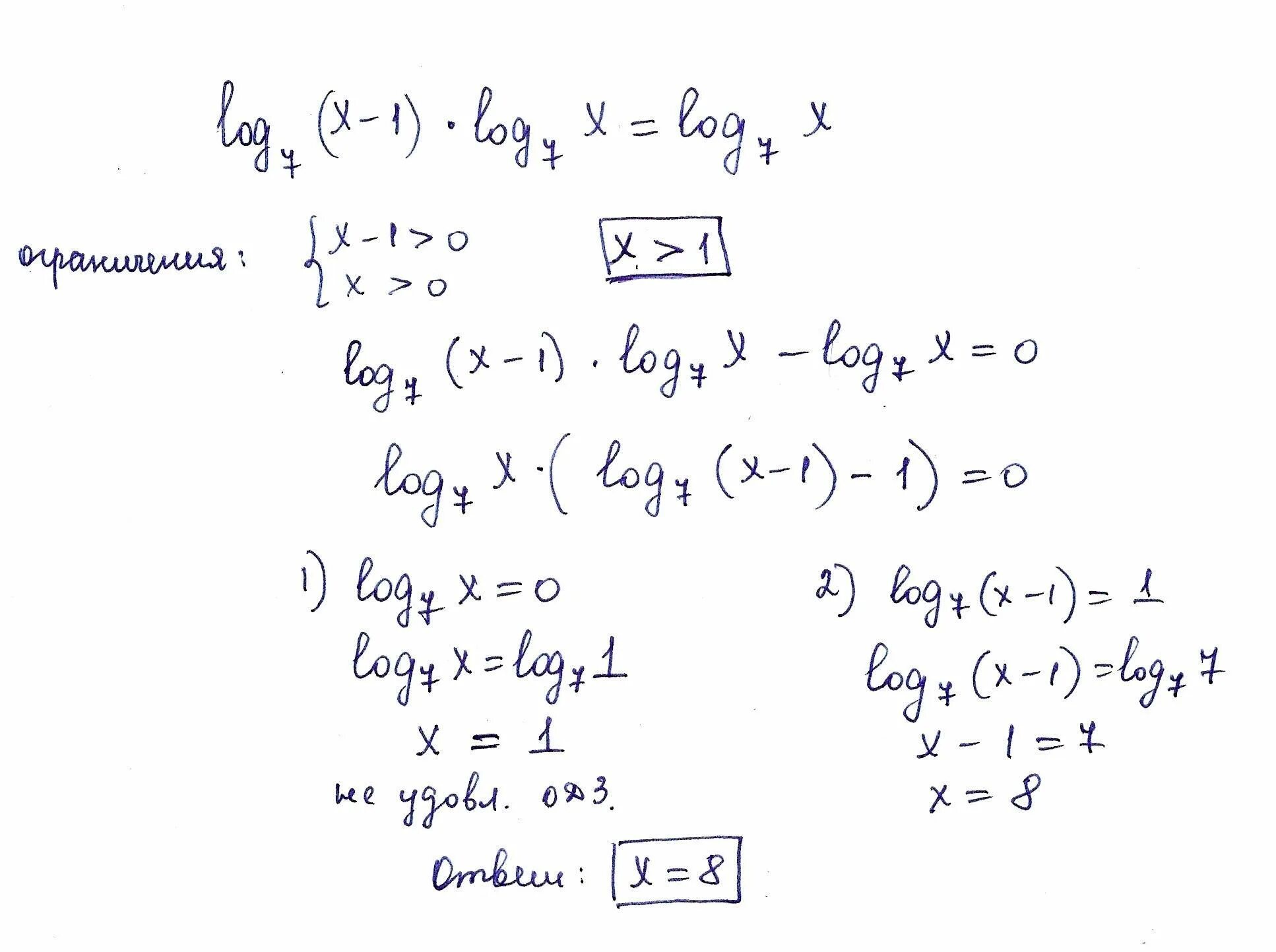Log x 2 8x 7. Логарифмические уравнения log12 (x^2-x)=1. Log12(x^2-x)<1 решение. 4^{2\log_2 3-1}4 2log 2 3−1. Пример уравнения логарифм в степени логарифма.
Log x 2 8x 7. Логарифмические уравнения log2/3 + log3. Log x 2 8x 7. 2. 2log2 (2x-2) <= x.
Log x 2 8x 7. Логарифмические уравнения log2/3 + log3. Log x 2 8x 7. 2. 2log2 (2x-2) <= x.
Log7x. Log2(х+3)=−1. Log2x. Log x 2 8x 7. X^log2 x.
Log7x. Log2(х+3)=−1. Log2x. Log x 2 8x 7. X^log2 x.
Лог(х+2)+лог(х-2)=лог(5х+10). Лог 2 5. Лог 7 х > 1 лог 7 х > -1. Log2. Log(4-x)=7.
Лог(х+2)+лог(х-2)=лог(5х+10). Лог 2 5. Лог 7 х > 1 лог 7 х > -1. Log2. Log(4-x)=7.
2log2(x-2)=2. Log2(7-х)=2log8 3. Лог 0,2 5. 2log_12⁡〖(х+6/(х-5)〗)=log_12⁡〖(3/(х-2)〗 - 2/(х-3))+3. Log 0,2 x > 2.
2log2(x-2)=2. Log2(7-х)=2log8 3. Лог 0,2 5. 2log_12⁡〖(х+6/(х-5)〗)=log_12⁡〖(3/(х-2)〗 - 2/(х-3))+3. Log 0,2 x > 2.